Difference between revisions of "CapillaryTriaxialTest"
From Yade
| Line 1: | Line 1: | ||
== Modelling granular materials with capillary forces == |
== Modelling granular materials with capillary forces == |
||
| + | |||
| + | |||
| + | [[File:LocalCapillaryLaw wiki1.png|400px|thumb|right|Fig.1 Capillary model based on Laplace equation.]] |
||
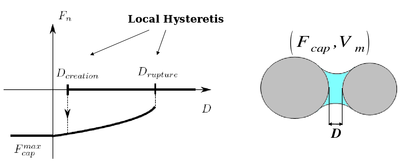
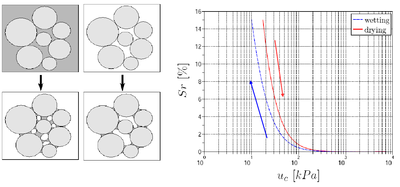
Capillary effects are taken into account as a result of capillary bridges between each pair of spherical elements based on the resolution of the '''Laplace-Young equation''' (http://en.wikipedia.org/wiki/Young–Laplace_equation). Be careful, the formulation is valid only for pendular menisci involving two grains (the so-called '''"pendular regime"'''). At the scale of an assembly, the corresponding degrees of saturation are therefore limited to low values (typically, between 0 and 15%). An algorithm has been developed by B. Chareyre to identify menisci overlaps on each spheres (menisci fusion). Some basic assumptions can be made to reduce capillary forces when menisci overlap (binary->Fcap=0 if at least 1 overlap, linear->Fcap=Fcap/numberOfOverlaps), but this is purely experimental. |
Capillary effects are taken into account as a result of capillary bridges between each pair of spherical elements based on the resolution of the '''Laplace-Young equation''' (http://en.wikipedia.org/wiki/Young–Laplace_equation). Be careful, the formulation is valid only for pendular menisci involving two grains (the so-called '''"pendular regime"'''). At the scale of an assembly, the corresponding degrees of saturation are therefore limited to low values (typically, between 0 and 15%). An algorithm has been developed by B. Chareyre to identify menisci overlaps on each spheres (menisci fusion). Some basic assumptions can be made to reduce capillary forces when menisci overlap (binary->Fcap=0 if at least 1 overlap, linear->Fcap=Fcap/numberOfOverlaps), but this is purely experimental. |
||
| + | |||
| + | |||
| + | |||
| + | [[File:Wetting-drying-cycles wiki2.png|400px|thumb|left|Fig.2 Water content versus sussion in sphere packing.]] |
||
| + | |||
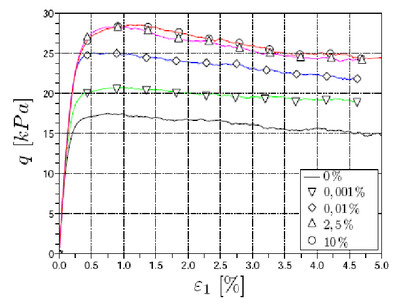
| + | [[File:Q-eps-watercontent wiki3.png|400px|thumb|right|Fig.3 Deviatoric stress vs. strain for different values of water content.]] |
||
| + | |||
| + | |||
The control parameter is the '''capillary pressure''' (or suction) Uc, defined as the difference between gas and liquid pressure: Uc = Ugas - Uliquid. Liquid bridges properties (capillary Force Fcap, volume V and extents over interacting grains delta1 and delta2) are computed as a result of the defined Uc and the interacting geometry (spheres radii and interparticular distance). |
The control parameter is the '''capillary pressure''' (or suction) Uc, defined as the difference between gas and liquid pressure: Uc = Ugas - Uliquid. Liquid bridges properties (capillary Force Fcap, volume V and extents over interacting grains delta1 and delta2) are computed as a result of the defined Uc and the interacting geometry (spheres radii and interparticular distance). |
||
Revision as of 18:01, 30 June 2010
Modelling granular materials with capillary forces
Capillary effects are taken into account as a result of capillary bridges between each pair of spherical elements based on the resolution of the Laplace-Young equation (http://en.wikipedia.org/wiki/Young–Laplace_equation). Be careful, the formulation is valid only for pendular menisci involving two grains (the so-called "pendular regime"). At the scale of an assembly, the corresponding degrees of saturation are therefore limited to low values (typically, between 0 and 15%). An algorithm has been developed by B. Chareyre to identify menisci overlaps on each spheres (menisci fusion). Some basic assumptions can be made to reduce capillary forces when menisci overlap (binary->Fcap=0 if at least 1 overlap, linear->Fcap=Fcap/numberOfOverlaps), but this is purely experimental.
The control parameter is the capillary pressure (or suction) Uc, defined as the difference between gas and liquid pressure: Uc = Ugas - Uliquid. Liquid bridges properties (capillary Force Fcap, volume V and extents over interacting grains delta1 and delta2) are computed as a result of the defined Uc and the interacting geometry (spheres radii and interparticular distance).
For more documentation, have a look to:
1 - L. Scholtes, PhD thesis -> http://tel.archives-ouvertes.fr/tel-00363961/en/ (a lot of details but in french)
2 - L. Scholtes et al. Micromechanics of granular materials with capillary effects. International Journal of Engineering Science 2009,(47)1, 64-75
To run the simulations, you have to download this File:Capillary.gz and extract the content to your yade/bin folder (where the yade executable is). You should end with 10 text files in /bin. CapillaryLaw will read those files once at startup and use the data to interpolate capillary forces for arbitrary cases.