Difference between revisions of "CapillaryTriaxialTest"
From Yade
| Line 14: | Line 14: | ||
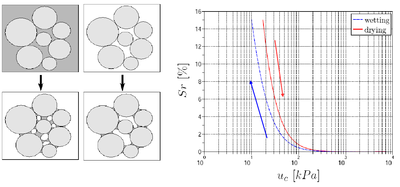
The control parameter is the '''capillary pressure''' (or suction) Uc, defined as the difference between gas and liquid pressure: Uc = Ugas - Uliquid. Liquid bridges properties (capillary Force Fcap, volume V and extents over interacting grains delta1 and delta2) are computed as a result of the defined Uc and the interacting geometry (spheres radii and interparticular distance). |
The control parameter is the '''capillary pressure''' (or suction) Uc, defined as the difference between gas and liquid pressure: Uc = Ugas - Uliquid. Liquid bridges properties (capillary Force Fcap, volume V and extents over interacting grains delta1 and delta2) are computed as a result of the defined Uc and the interacting geometry (spheres radii and interparticular distance). |
||
| − | + | '''Examples''' can be found in examples/capillaryLaplaceYoung source folder. Also, for more '''documentation''', have a look at: |
|
1 - L. Scholtes, PhD thesis -> http://tel.archives-ouvertes.fr/tel-00363961/en/ (a lot of details but in french) |
1 - L. Scholtes, PhD thesis -> http://tel.archives-ouvertes.fr/tel-00363961/en/ (a lot of details but in french) |
||
Revision as of 19:11, 21 September 2016
Modelling granular materials with capillary forces
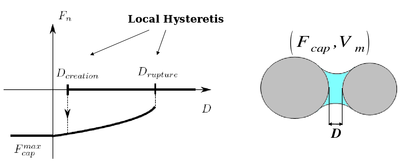
Capillary effects are taken into account as a result of capillary bridges between each pair of spherical elements based on the resolution of the Laplace-Young equation (http://en.wikipedia.org/wiki/Young–Laplace_equation). Be careful, the formulation is valid only for pendular menisci involving two grains (the so-called "pendular regime"). At the scale of an assembly, the corresponding degrees of saturation are therefore limited to low values (typically, between 0 and 15%). An algorithm has been developed by B. Chareyre to identify menisci overlaps on each spheres (menisci fusion). Some basic assumptions can be made to reduce capillary forces when menisci overlap (binary->Fcap=0 if at least 1 overlap, linear->Fcap=Fcap/numberOfOverlaps), but this is purely experimental.
The control parameter is the capillary pressure (or suction) Uc, defined as the difference between gas and liquid pressure: Uc = Ugas - Uliquid. Liquid bridges properties (capillary Force Fcap, volume V and extents over interacting grains delta1 and delta2) are computed as a result of the defined Uc and the interacting geometry (spheres radii and interparticular distance).
Examples can be found in examples/capillaryLaplaceYoung source folder. Also, for more documentation, have a look at:
1 - L. Scholtes, PhD thesis -> http://tel.archives-ouvertes.fr/tel-00363961/en/ (a lot of details but in french)
2- Scholtès, L., Chareyre, B., Nicot, F., Darve, F. (2009), Micromechanics of granular materials with capillary effects. International Journal of Engineering Science (47), pages 64–75. DOI 10.1016/j.ijengsci.2008.07.002
3 - Scholtès, L., Hicher, P.-Y., Chareyre, B., Nicot, F., Darve, F. (2009), On the capillary stress tensor in wet granular materials. International Journal for Numerical and Analytical Methods in Geomechanics (33), pages 1289–1313. DOI 10.1002/nag.767
4 - Scholtès, L., Chareyre, B., Nicot, F., Darve, F. (2009), Discrete modelling of capillary mechanisms in multi-phase granular media. Computer Modeling in Engineering and Sciences (52), pages 297–318. DOI ` <http://dx.doi.org/>`_
5- Duriez J., Wan R. (2016), Contact angle mechanical influence in wet granular soils, Acta Geotechnica (currently under review)
To run the simulations, you need 10 text files ("capillary files") located in whatever path you start Yade from (yade/install/bin, typically). Law2_ScGeom_CapillaryPhys_Capillarity will read those files once at startup and use the data to interpolate capillary forces for arbitrary values of suction and particles sizes. A set of files considering a null wetting (contact) angle can be downloaded here Alternatively, .m scripts are provided in examples/capillaryLaplaceYoung source folder in order for you to generate your own set of files (e.g., for other wetting angle).
In any case, the data files are numerically established, leading to a finite precision: the highest suction values triggering meniscii failure are approximated. Then, for e.g. a pair of monosized contacting grains, physical meniscii with a filling angle smaller than 2 degrees can not be described. The corresponding limit adimensionned suction is around 1500. As such, simulations using adimensionned suction values greater than 1500 are (little) impacted by the precision of the data files. The code issues a warning message in such case.